We all learn differently, so some of us need a slightly different approach to get the most out of our LSAT studies. In this series, we’ll cover LSAT techniques that work particularly well for visual learners. Rather than learning and memorizing rules, these techniques will put your pencil and paper to work, allowing you to map out and visualize the correct answer.
Quantifiers? Quantity statements? “Most” and “some” statements? Whatever you call this part of the LSAT, it shows up enough on the Logical Reasoning section that we feel compelled to learn it. It can be the difference between a quick couple of points and an agonizing, time-wasting couple of questions. And when Logical Reasoning will account for two-thirds of our final score in August 2024, we’ll be behooved — totally, utterly, full of hooves — to learn this skill.
So, what is this skill? It involves combining an “if-then” statement (AKA a “conditional statement”) with a “most” or “some” statement to reach a valid conclusion. You may get a Must Be True question that provides an “if-then” premise and a “most” or “some” premise, and the correct answer will be a valid combination of those two premises. You may get a Parallel or Flawed Parallel Reasoning question that provides an argument that combines an “if-then” premise and a “most” or “some” premise to reach a conclusion, and you’ll be tasked with identifying the answer choice that features an argument that matches that argument’s structure and reaches a similarly valid or invalid conclusion. Or, you may get a Strengthen with a Sufficient Premise question (AKA a Sufficient Assumption question) that features a “most” or “some” premise and conclusion, and we’ll have to find the additional premise that we can connect to the initial premise and validly draw the conclusion.
Most LSAT prep companies take a very formulaic approach to this topic. That makes sense because this topic is adjacent to — for most of us, uncomfortably adjacent to — math. But for many of us, it’s scary and difficult to wade into the rough waters of mathematics. Visual learners, especially, find the rule-based approach recommended by most LSAT prep companies a little challenging to wrap their heads around. So, let’s propose an alternative approach for visualizers — one that harnesses the power of a notable mathematic shape: the triangle.
In fact, we’ll call this approach the “Triangle Method” — shout out Sam Barry, Tex Winter, and Phil Jackson — to honor this powerful shape. How does it work?
Let’s take a few examples. We’ll start by using this method to combine an “if-then” statement with a “some” statement.
Example 1: “Some raccoons subsist on garbage exclusively. All raccoons are intelligent, noble creatures.”
We’ll start by diagramming both statements. To diagram the “some” statement, we’ll connect the two conditions — “raccoons” and “subsist on garbage” — with a double-sided arrow with an “s” in the middle. (We use a double-sided arrow to show that this term is reversible.) To diagram the “all” statement, we’ll translate it into an “if-then” claim (“If a creature is a raccoon, it is intelligent and noble”) and put the “if” part on the left side of an arrow and the “then” part on the right. Make sure the arrow points to the “then” part.

Then, we’ll take the “if-then” statement and keep it horizontal. We’ll then connect the “some” part to the “if-then” statement. We’ll take the part that the two statements share — in this case, “Raccoon” — and attach the other part at a 90° angle. Here’s what that looks like:

We have the two sides of the triangle formed. Now, we just need to form the third side. That third side is going to allow us to draw a conclusion. But, when we’re using the triangle to connect “most” and “some” statements, we can only draw a valid conclusion when the vertical line is on the left side. If it were on the right side, we couldn’t draw a valid conclusion. In this case, the vertical line is on the left, so we can draw a conclusion when connecting “Subsist on Garbage” and “Intelligent/Noble.” We’ll connect those points with another double-sided arrow with an “s” in the middle:
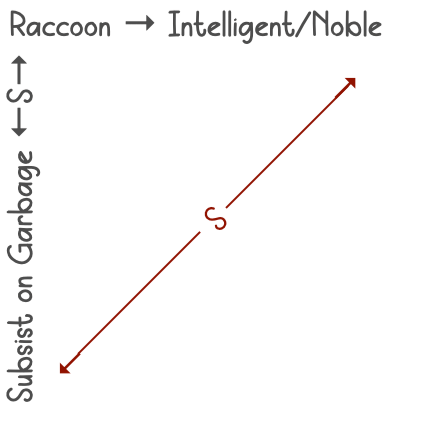
So, the valid conclusion we can draw is that “Subsist on Garbage ←S→ Intelligent/Noble.” Or, put another way, “Some creatures that subsist on garbage are intelligent and noble.” These “some” statements are reversible, so we could also claim that, “Some intelligent and noble creatures subsist on garbage.”
But remember, the vertical part needs to be on the left side of the triangle to make a valid conclusion. Let’s take this example …
Example 2: “All lawyers took the LSAT. Some people who take the LSAT hated quantifiers.”
Again, we’ll start by diagramming the two claims …

And again, we’ll keep the “if-then” claim horizontal and attach the other claim to the shared term at a 90° angle:
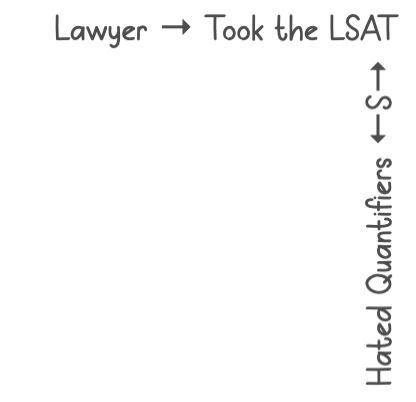
Unlike Example 1, the vertical part is on the right side of the triangle. When this happens, we can’t draw a valid conclusion. So, we cannot say that “Lawyers ←S→ Hated Quantifiers” or “Some lawyers hated quantifiers.” Perhaps only those who liked quantifiers went on to become lawyers!
And this is the difference that allows us to visualize when we can and cannot make valid conclusions. When the triangle looks like Example 1, we can draw a valid conclusion. When the triangle looks like Example 2, we cannot. See the difference?
Let’s try another example. This time, we’ll combine an “if-then” statement with a “most” statement.
Example 3: “Most U.S. presidents are lawyers. All U.S. presidents work for the citizens.”
Again, start by diagramming both statements. To diagram the “most” statement, we’ll connect the two conditions — “U.S. presidents” and “lawyers” — with an “m”-arrow that points to the right (We won’t use a double-sided arrow because these “most” statements are not reversible.) To diagram the “all” statement, we’ll translate it into an “if-then” claim (“If one is a U.S. president, then one works for the citizens”) and put the “if” part on the left side of an arrow and the “then” part on the right. Again, make sure the arrow points to the “then” part.

Same steps as before. We’ll keep the “if-then” horizontal. We’ll then connect the “most” part to the “if-then” statement. We’ll use the part that the two statements share — in this case, “U.S. President” — and attach the other part at a 90° angle. Here’s what we get:

We have two sides of the triangle, and now we’ll complete the triangle to draw the conclusion. Again, we can only draw a valid conclusion if the vertical line is on the left side. That condition is satisfied, so we can draw a valid conclusion.
But with “most” statements, we have one more test. We need to check whether the “m”-arrow is pointing up or down. If it’s pointing down, we need to decrease the strength of our conclusion from a “most” to a “some” conclusion. That’s the case here, so we’ll connect “Lawyer” and “Works for Citizens” with a double-sided “s”-arrow:
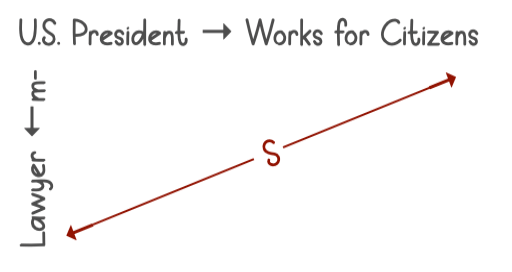
We can conclude that “Laywer ←S→ Work for Citizens” or “Some lawyers work for the citizens” (or “Some people who work for the citizens are lawyers”).
Let’s take a look at another example …
Example 4: “Most songs are just OK. Anything that is just OK is not worth revisiting.”
You know the drill — diagram the two statements …

… keep the “if-then” statement horizontal and connect the other one using the shared term:

Again, we have two sides of the triangle and the vertical line is on the left side. So, we can complete the triangle and draw the conclusion.
But unlike Example 4, the “m”-arrow is pointing up. If it’s pointing up, we don’t have to decrease the strength of our conclusion from a “most” to a “some” conclusion. We can make the conclusion a “most” statement. So, we’ll connect “Songs” and “Not Worth Revisiting” with an “m”-arrow:
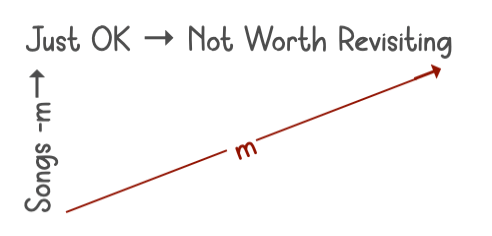
So, we can conclude “Songs -m→ Not Worth Revisiting” or “Most songs are not worth revisiting.” (Note that, unlike the “some” conclusions, we can’t reverse this one.)
Let’s try one more “all” and “most” …
Example 5: “All chocolate has bitter flavor notes. Most things with bitter flavor notes are hated by children.”
We’ll diagram out the claims …

… and then keep the “if-then” statement horizontal and connect the other one using the shared term:

But, alas, the vertical line is on the right side. So, we cannot draw a valid conclusion here.
Finally, let’s cover one more type of conclusion we can draw — the combination of two “most” statements.
Example 6: “Most dogs are loyal to their owners. Most dogs will show more affection to strangers than their owners.”
Once again, we’ll start by diagramming these two claims:

Then, we’ll keep one of the two claims horizontal. When both are “most” statements, it doesn’t matter which we choose. Then, we’ll attach the other claim at a 90° angle:

We can draw a valid conclusion because the vertical line is on the left. But combining two “most” statements entails another requirement: the “m”-arrow must point down. That is true here. And we need to make that conclusion a weaker “some” statement because the “m”-arrow is pointing down. So, we can conclude:

So, we can conclude that “More Affectionate to Strangers ←S→ Loyal to Owners” or “Some creatures that are more affectionate to strangers are loyal to their owners” (or “Some creatures that are loyal to their owners are more affectionate to strangers”).
One final example!
Example 7: “Most cats can jump really high. Most creatures who can jump really high like to eat leaves.”

We’ll take either claim and make it the horizontal line. But if we make the “Cats -m→ Jump Really High” part horizontal, the vertical line will be on the right side, preventing us from making the conclusion:

On the other hand (or, paw, as it were), if we make the “Jump Really High -m→ Like to Eat Leaves” part horizontal, the “m”-arrow will point up, which prevents us from drawing a conclusion when combining two “most” statements:

Either way, we can’t draw a valid conclusion.
If you’d like more practice with these, check out our Office Hours session on this topic. You’ll need to subscribe to the LSATMax full course or Office Hours course to access this lesson.
Hopefully, these triangles will help you visualize which conclusions you can and cannot draw out when combining “if-then” statements with quantifiers like “most” and “some.” Stay tuned for more techniques for visual learners!